Family: cumulative
Links: mu = probit; disc = identity
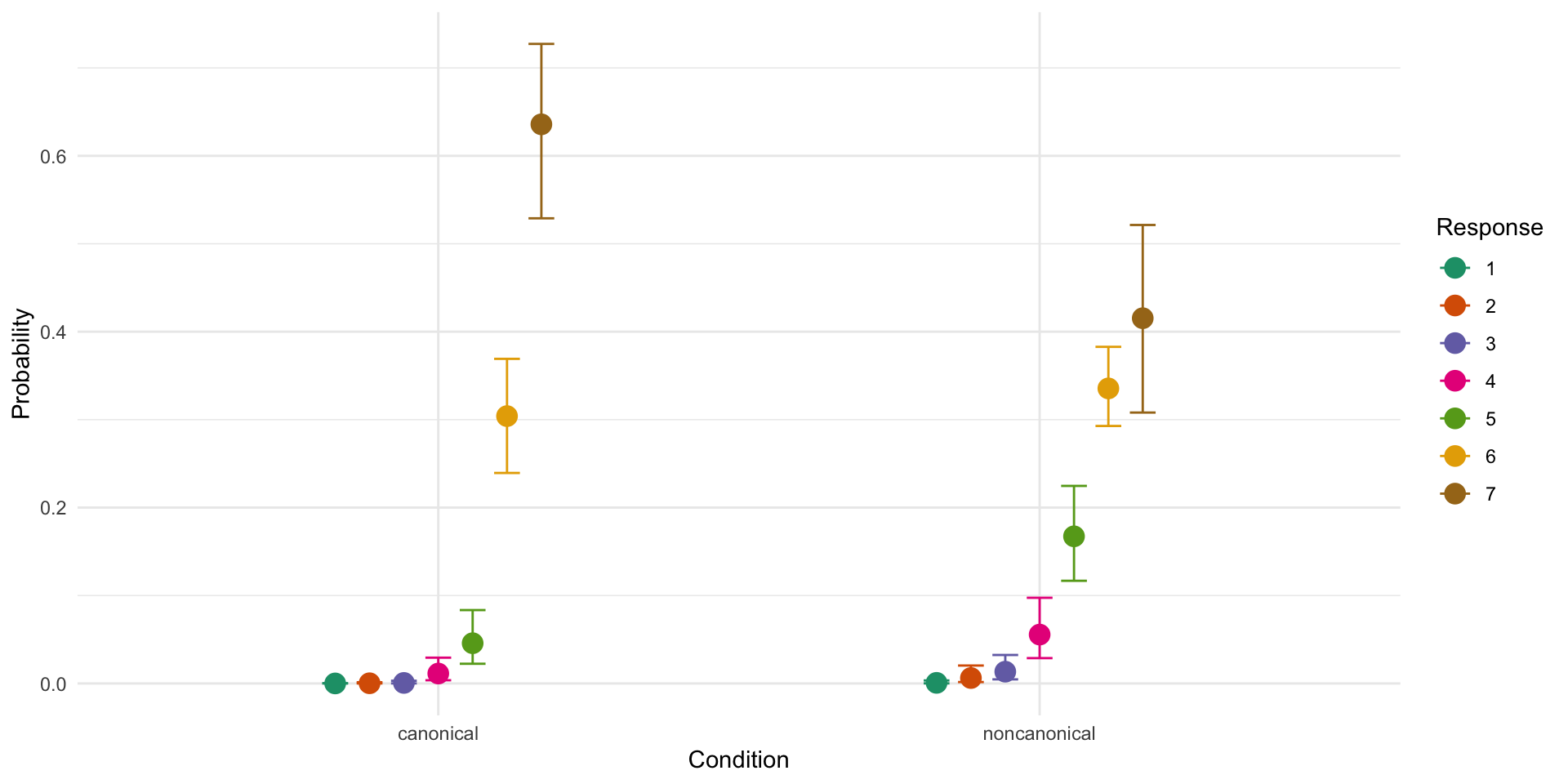
Formula: Response ~ Condition + (Condition | Participant) + (1 | Item)
Data: acceptability (Number of observations: 1176)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Multilevel Hyperparameters:
~Item (Number of levels: 28)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.36 0.07 0.25 0.50 1.00 1430 1825
~Participant (Number of levels: 42)
Estimate Est.Error l-95% CI u-95% CI Rhat
sd(Intercept) 0.89 0.13 0.68 1.18 1.00
sd(Conditionnoncanonical) 0.33 0.13 0.05 0.57 1.00
cor(Intercept,Conditionnoncanonical) -0.20 0.32 -0.76 0.49 1.00
Bulk_ESS Tail_ESS
sd(Intercept) 805 1735
sd(Conditionnoncanonical) 596 528
cor(Intercept,Conditionnoncanonical) 1823 1347
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
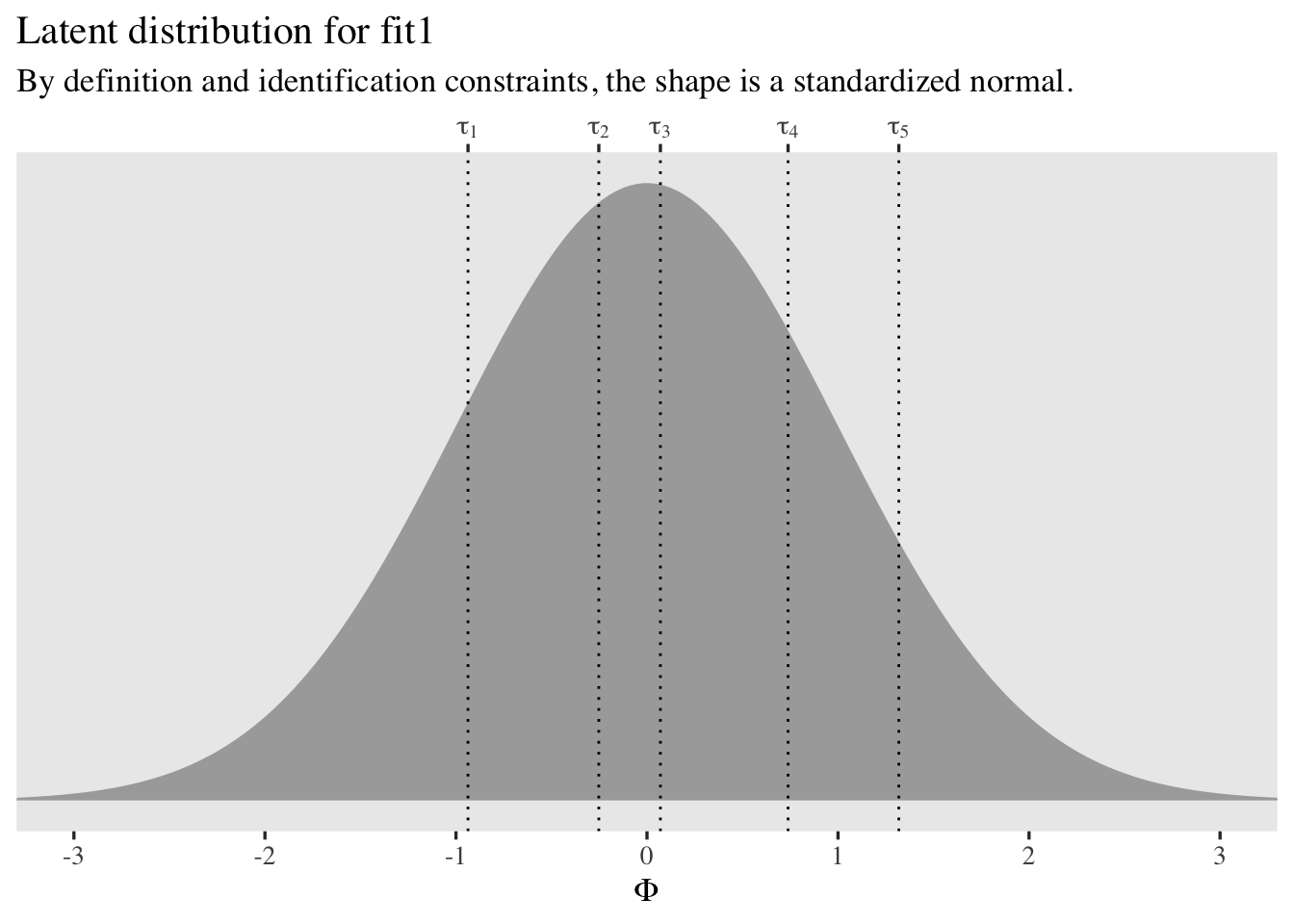
Intercept[1] -3.50 0.22 -3.94 -3.09 1.00 903
Intercept[2] -2.81 0.19 -3.18 -2.45 1.00 825
Intercept[3] -2.49 0.18 -2.86 -2.14 1.00 803
Intercept[4] -1.96 0.18 -2.32 -1.62 1.00 752
Intercept[5] -1.36 0.17 -1.70 -1.04 1.01 722
Intercept[6] -0.33 0.17 -0.65 -0.01 1.01 699
Conditionnoncanonical -0.70 0.09 -0.89 -0.53 1.00 2456
Tail_ESS
Intercept[1] 1876
Intercept[2] 1444
Intercept[3] 1444
Intercept[4] 1475
Intercept[5] 1350
Intercept[6] 1575
Conditionnoncanonical 2602
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
disc 1.00 0.00 1.00 1.00 NA NA NA
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).