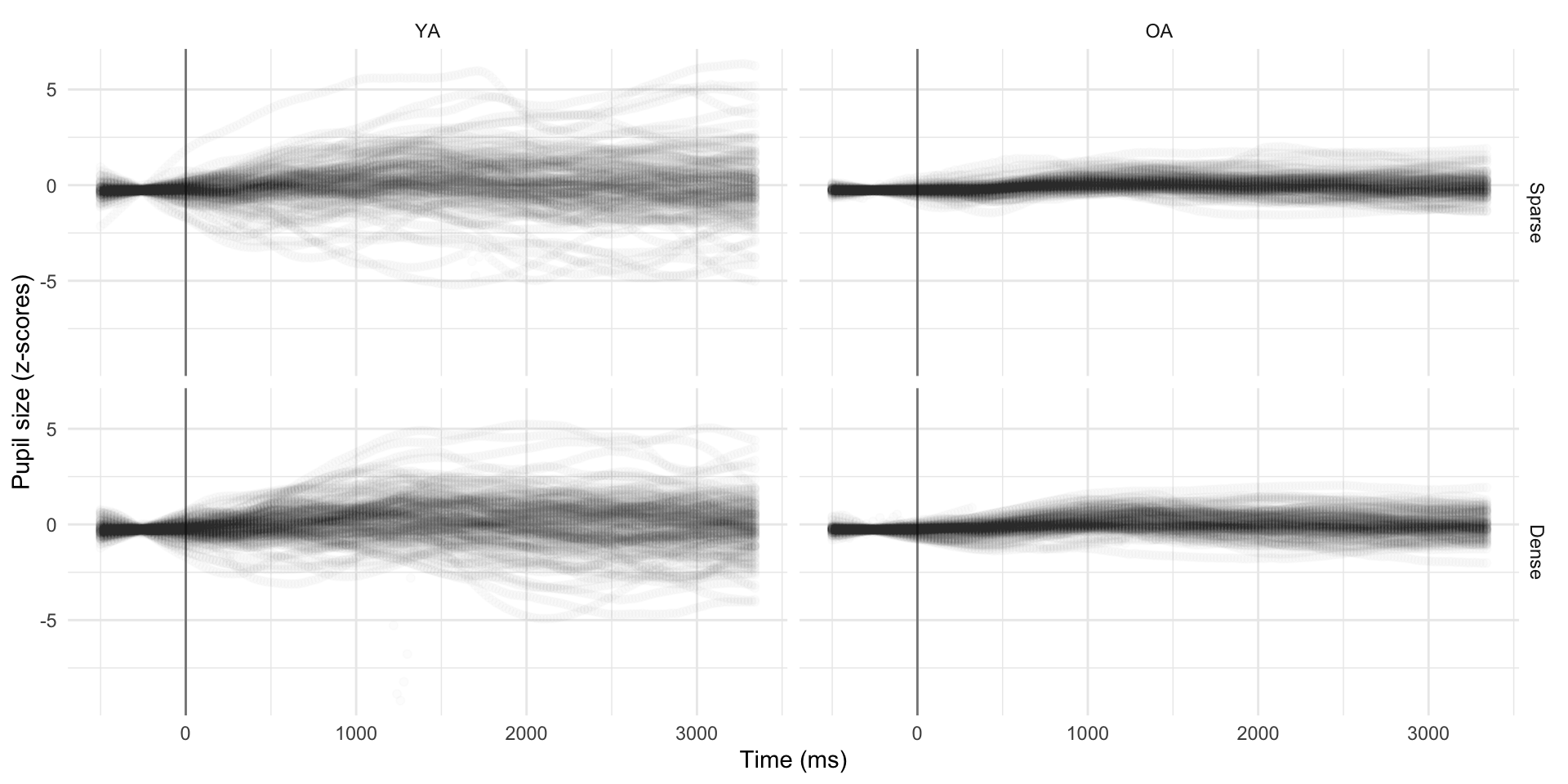
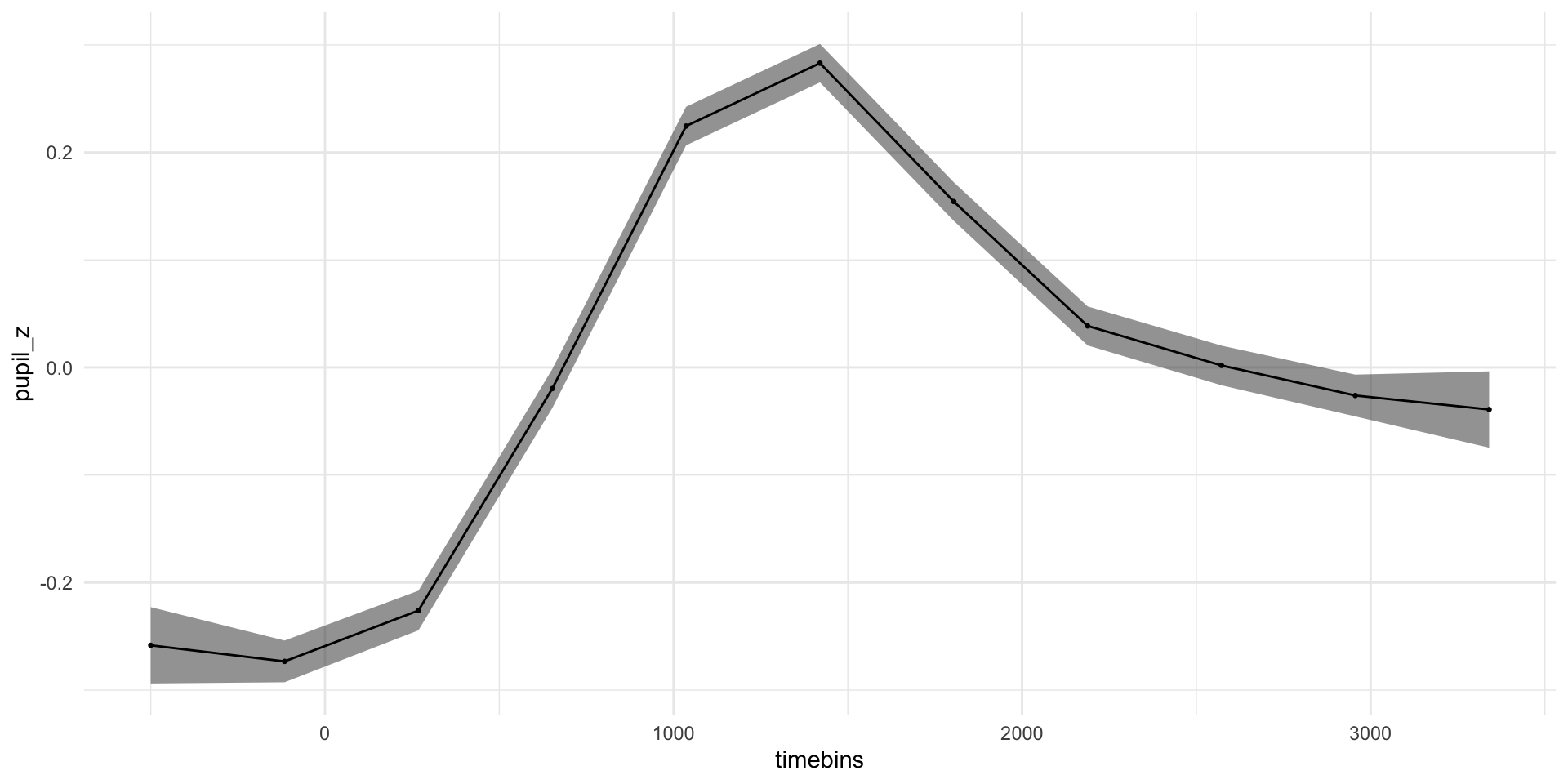
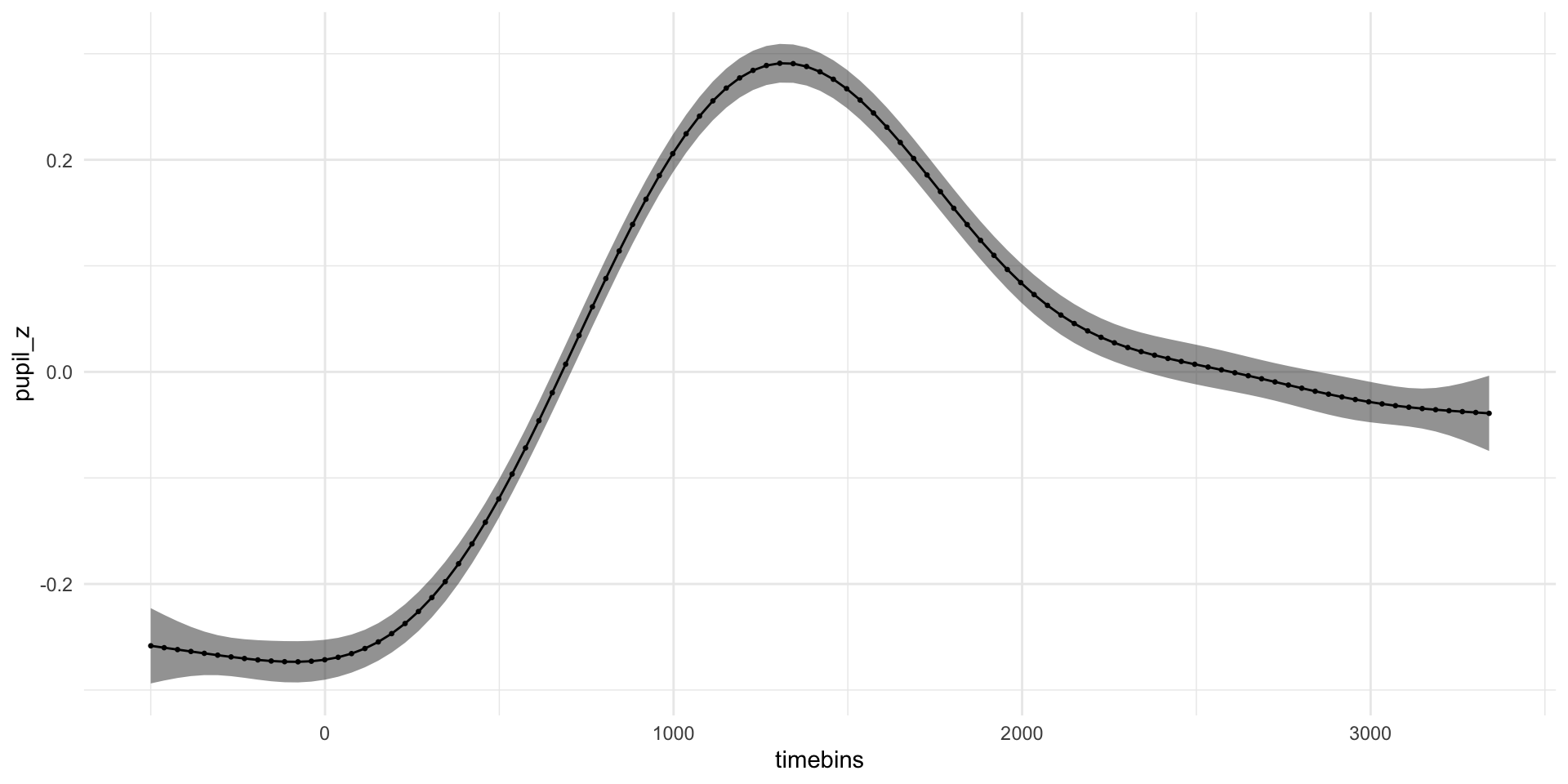
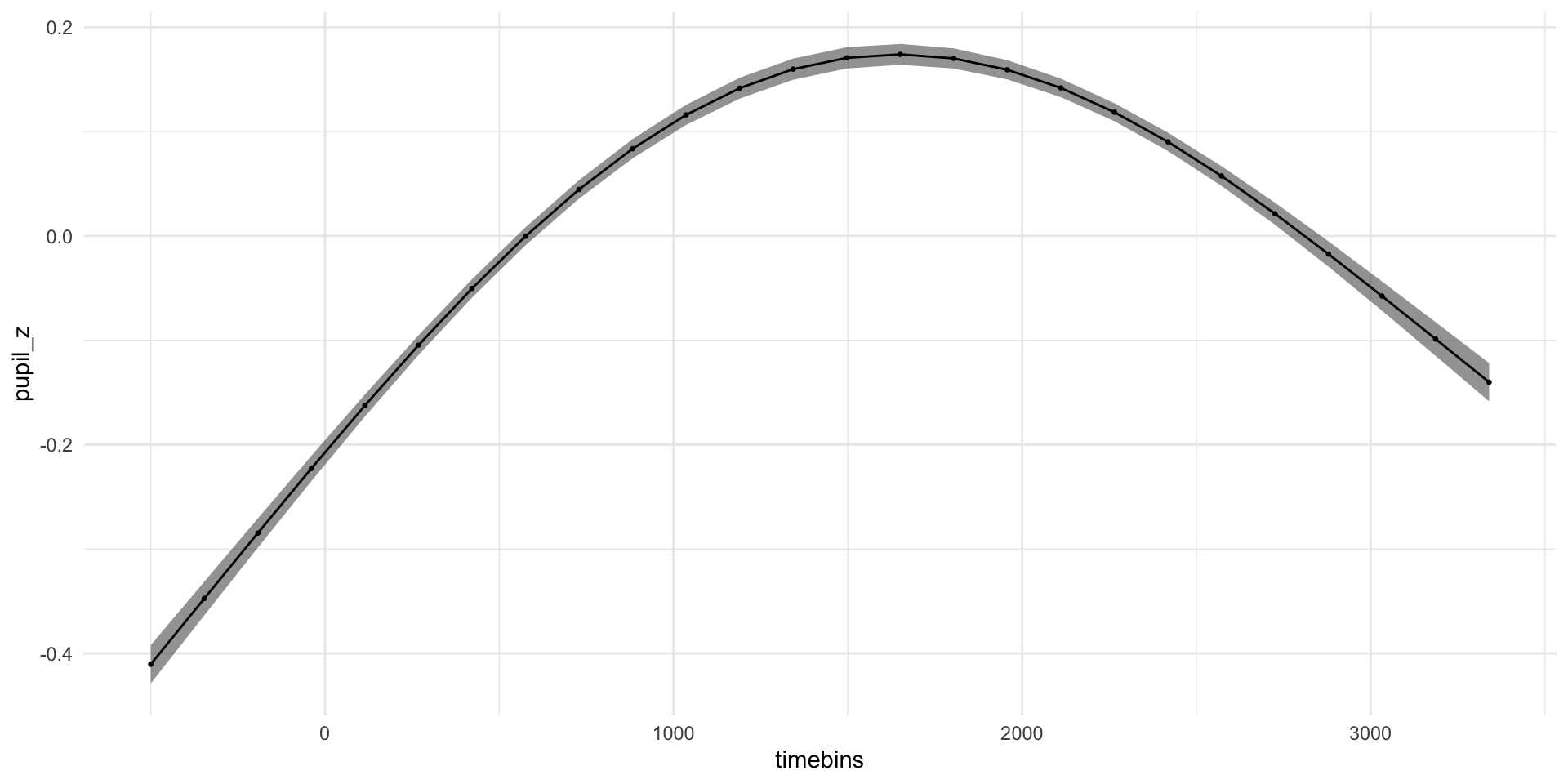
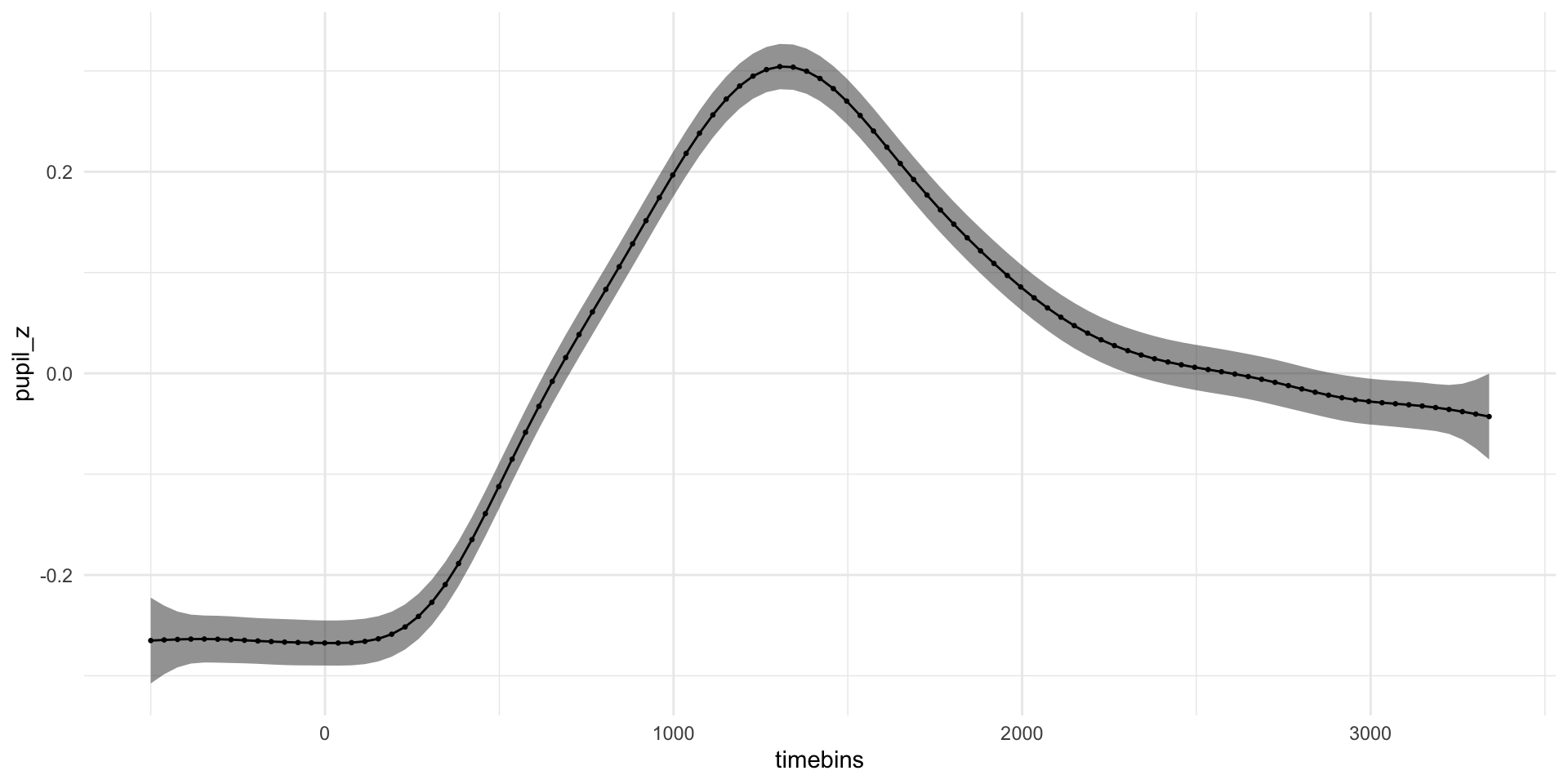
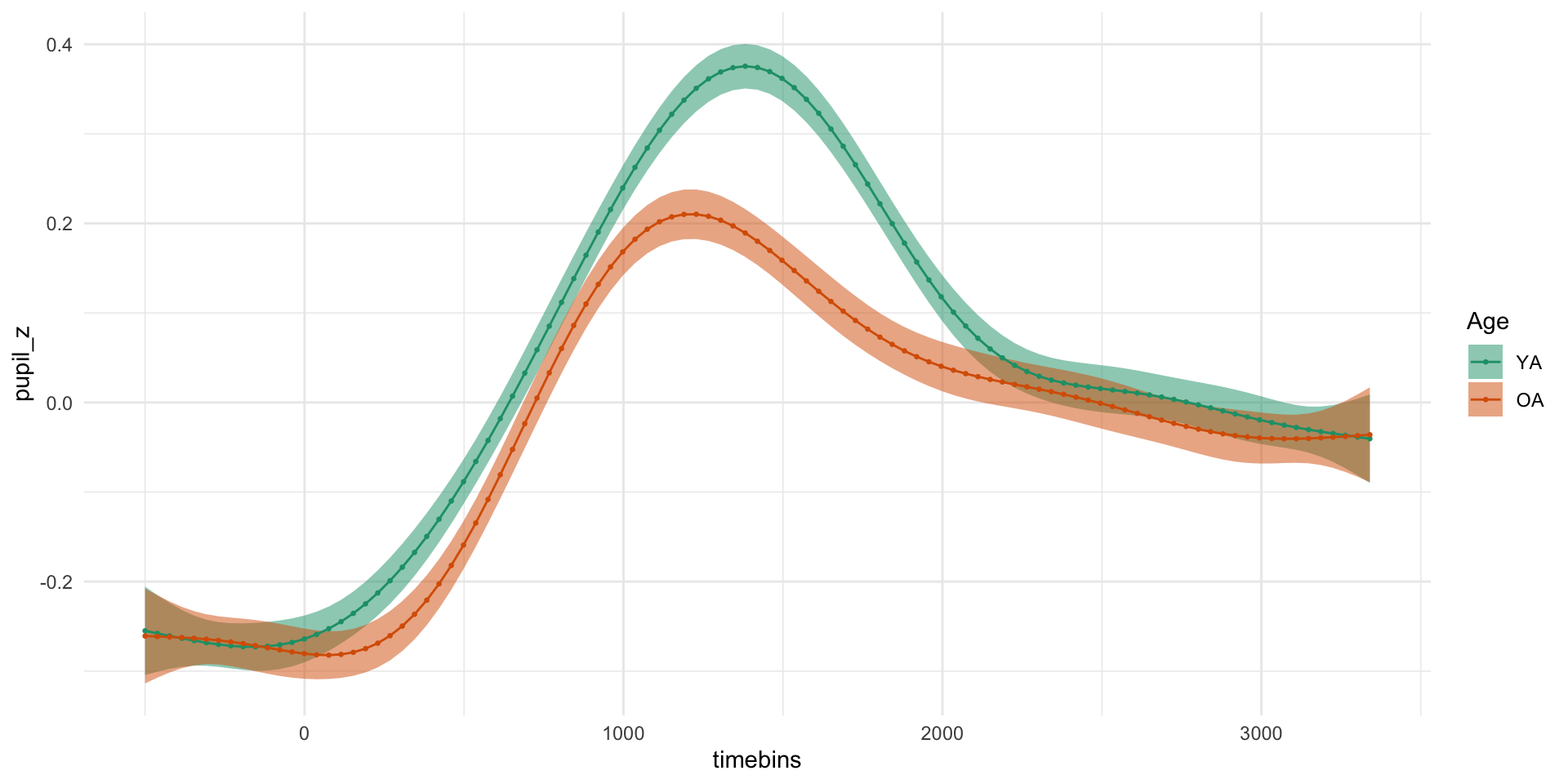
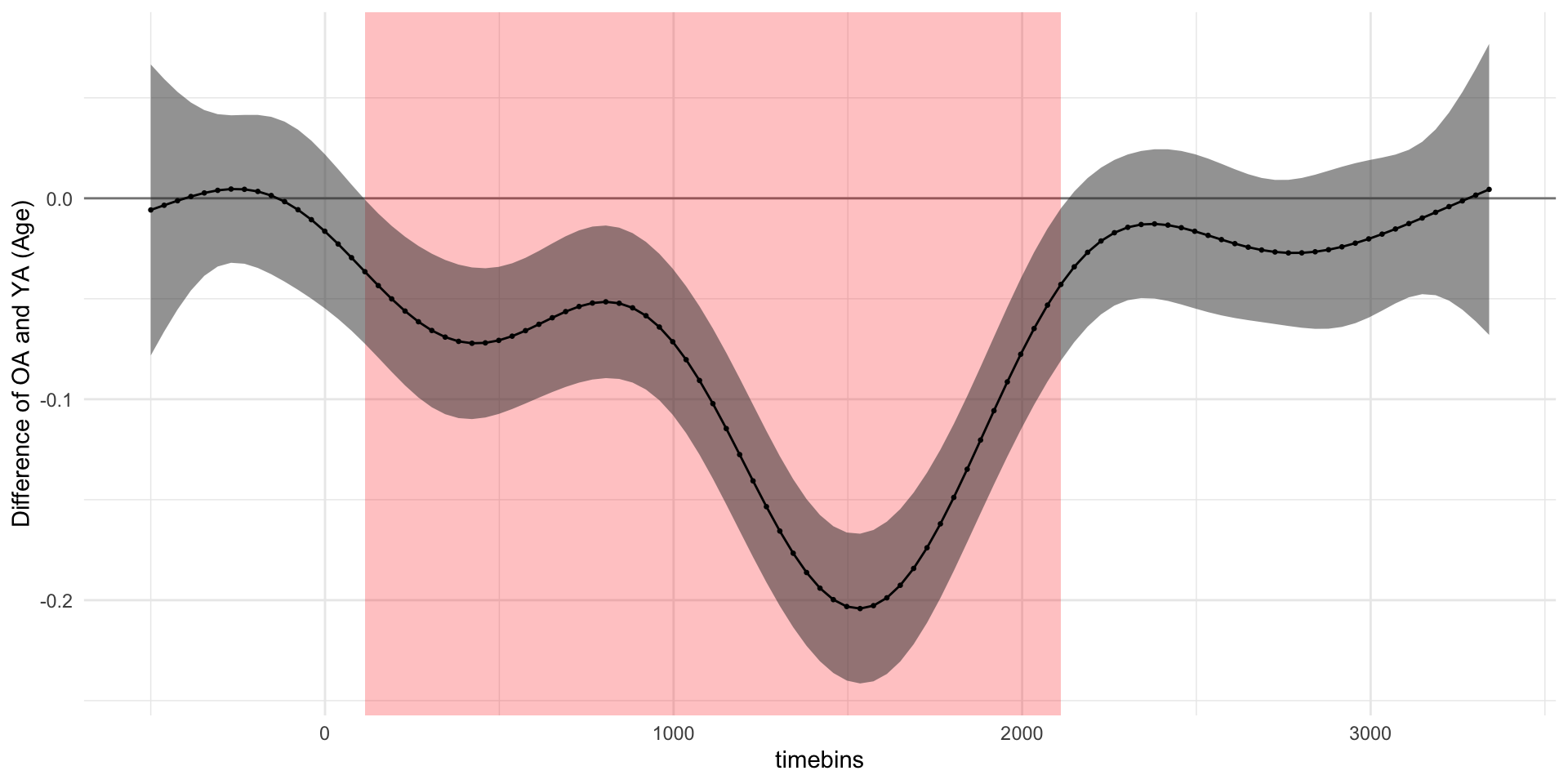
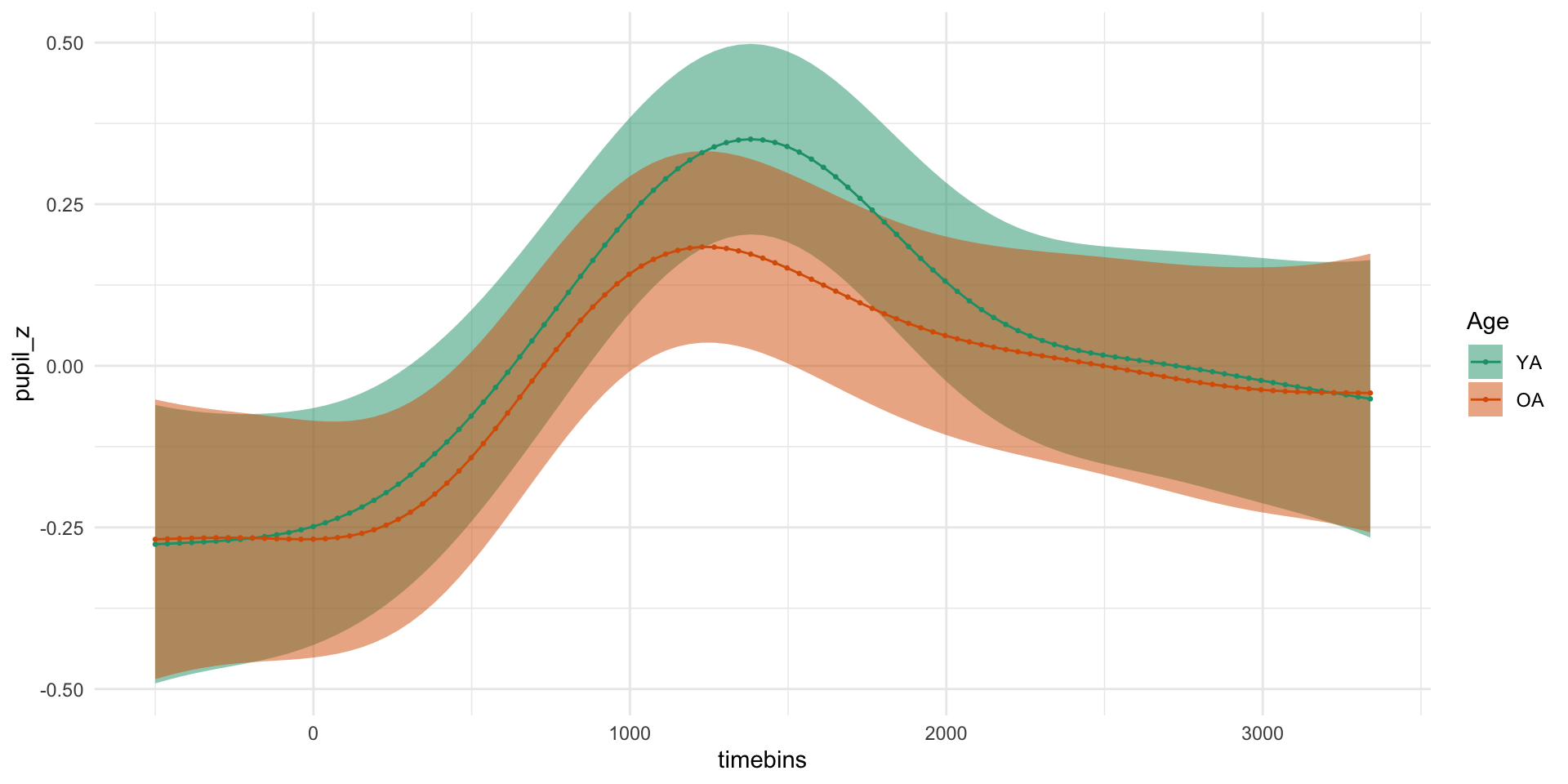
pdq_20 <- readRDS("data/pdq_20.rds") %>%
mutate(
Condition = factor(Condition, levels = c("Sparse", "Dense")),
Age = factor(Age, levels = c("YA", "OA")),
pupil_z = (pupil.binned - mean(pupil.binned)) / sd(pupil.binned)
)
pdq_20# A tibble: 88,008 × 8
subject trial Condition Age timebins Soundfile pupil.binned pupil_z
<dbl> <dbl> <fct> <fct> <dbl> <chr> <dbl> <dbl>
1 1 1 Sparse YA -500 NAMword_675_Mul… 84.5 0.00347
2 1 1 Sparse YA -480 NAMword_675_Mul… 75.8 -0.0239
3 1 1 Sparse YA -460 NAMword_675_Mul… 65.4 -0.0570
4 1 1 Sparse YA -440 NAMword_675_Mul… 54.3 -0.0922
5 1 1 Sparse YA -420 NAMword_675_Mul… 35.7 -0.151
6 1 1 Sparse YA -400 NAMword_675_Mul… 20.2 -0.200
7 1 1 Sparse YA -380 NAMword_675_Mul… 8.72 -0.237
8 1 1 Sparse YA -360 NAMword_675_Mul… 0.680 -0.262
9 1 1 Sparse YA -340 NAMword_675_Mul… -11.4 -0.300
10 1 1 Sparse YA -320 NAMword_675_Mul… -23.3 -0.338
# ℹ 87,998 more rows