03 - Regression models

Stefano Coretta

Vowel duration

# A tibble: 887 × 57
   index speaker file     rec_date        ipu   prompt word    time sentence_ons
   <dbl> <chr>   <chr>    <chr>           <chr> <chr>  <chr>  <dbl>        <dbl>
 1     1 it01    it01-001 29/11/2016 15:… ipu_1 Dico … pugu   0.990        0.990
 2     2 it01    it01-002 29/11/2016 15:… ipu_2 Dico … pada   3.62         0.502
 3     3 it01    it01-003 29/11/2016 15:… ipu_3 Dico … poco   6.13         0.697
 4     4 it01    it01-004 29/11/2016 15:… ipu_4 Dico … pata   8.82         0.623
 5     5 it01    it01-005 29/11/2016 15:… ipu_5 Dico … boco  11.5          0.665
 6     6 it01    it01-006 29/11/2016 15:… ipu_6 Dico … podo  14.3          0.647
 7     7 it01    it01-007 29/11/2016 15:… ipu_7 Dico … boto  17.2          0.740
 8     8 it01    it01-008 29/11/2016 15:… ipu_8 Dico … paca  19.7          0.502
 9     9 it01    it01-009 29/11/2016 15:… ipu_9 Dico … bodo  22.3          0.556
10    10 it01    it01-010 29/11/2016 15:… ipu_… Dico … pucu  24.8          0.535
# ℹ 877 more rows
# ℹ 48 more variables: sentence_off <dbl>, word_ons <dbl>, word_off <dbl>,
#   v1_ons <dbl>, c2_ons <dbl>, v2_ons <dbl>, c1_rel <dbl>, c2_rel <dbl>,
#   voicing_start <dbl>, voicing_end <dbl>, voicing_duration <dbl>,
#   voiced_points <dbl>, GONS <dbl>, max <dbl>, NOFF <dbl>, NONS <dbl>,
#   peak1 <dbl>, peak2 <dbl>, c1_duration <dbl>, c1_clos_duration <dbl>,
#   c1_vot <dbl>, c1_rvoff <dbl>, v1_duration <dbl>, c2_duration <dbl>, …

Vowel durations: plot

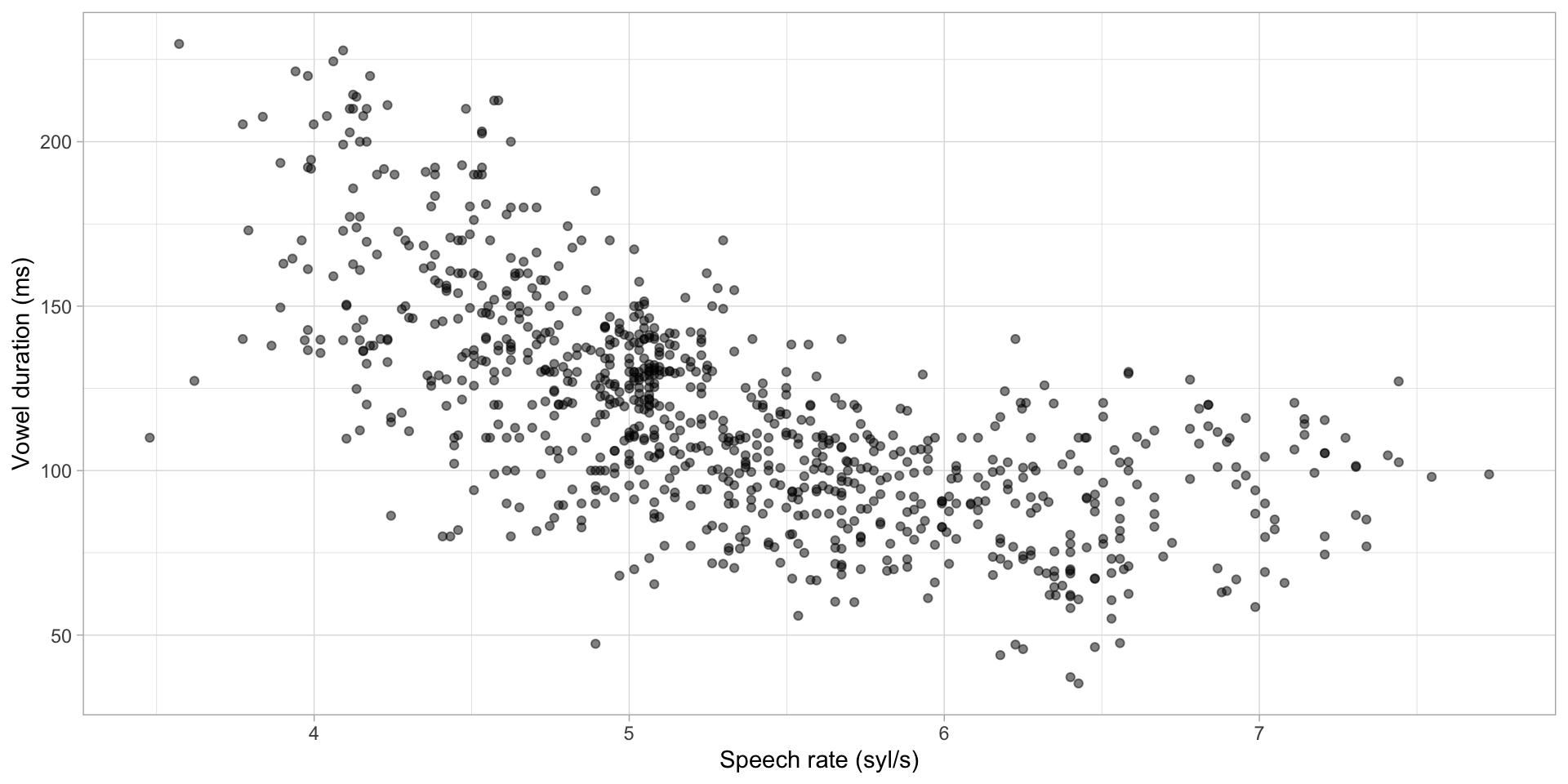
Figure 1: Vowel duration and speech rate.

A log-normal model of vowel duration

\[ dur \sim LogNormal(\mu, \sigma) \]

dur_logn <- brm(
  v1_duration ~ 1,
  family = lognormal,
  data = durations
)

But we want to investigate the relationship between speech rate and vowel duration!

Allow \(\mu\) to vary depending on speech rate

\[ \begin{align} dur_i & \sim LogNormal(\mu_i, \sigma)\\ \mu_i & = \beta_0 + \beta_1 \cdot SR_i\\ \end{align} \]

Does the formula for \(\mu\) ring a bell?

The formula of a line

\[ y = a + b \cdot x \]

  • \(a\) is the line’s intercept. This is \(y\) when \(x\) is 0.

  • \(b\) is the line’s slope (aka gradient). This is the change in \(y\) for every unit increase of \(x\).

See Linear models illustrated.

Regression model of vowel duration

\[ \begin{align} dur_i & \sim LogNormal(\mu_i, \sigma)\\ \mu_i & = \beta_0 + \beta_1 \cdot SR_i\\ \end{align} \]

  • \(\beta_0\) is the intercept. This is the mean vowel duration when speech rate is 0.

  • \(\beta_1\) is the slope. This is the change in vowel duration for each unit increase of speech rate (syl/s).

But…

Speech rate 0 doesn’t make sense!

  • Speech rate cannot be zero syllables per second.

We can centre speech rate.

  • Subtract the mean speech rate from all the speech rate values.

Centred speech rate

mean(durations$speech_rate, na.rm = TRUE)
[1] 5.314752
durations <- durations |> 
  mutate(
    speech_rate_c = speech_rate - mean(speech_rate, na.rm = TRUE)
  )
  • speach_rate_c = 0 means mean speech rate.

Centred speech rate: plot

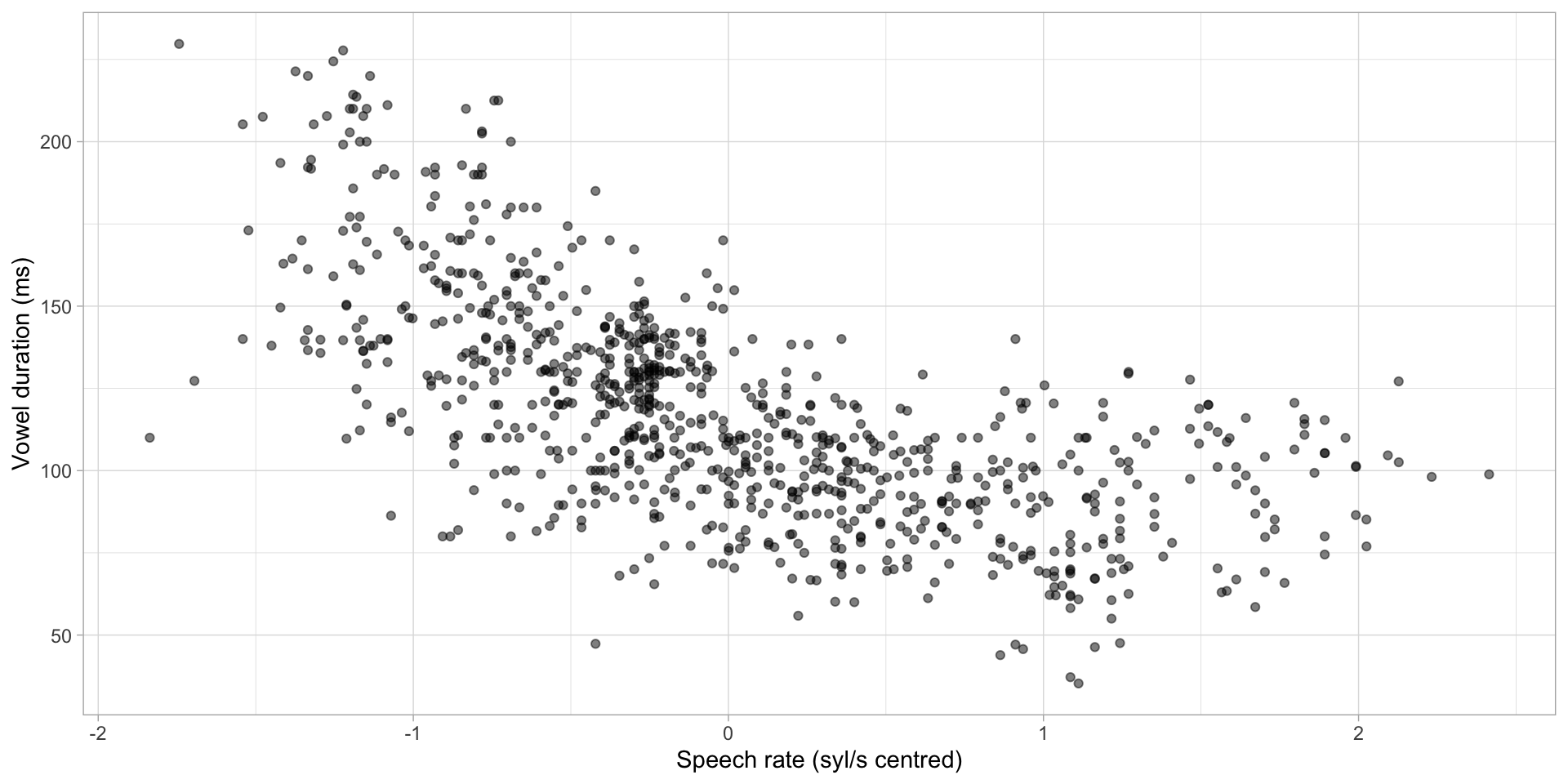
Figure 2: Vowel duration and (centred) speech rate.

Regression model of vowel durations: centred speech rate

\[ \begin{align} dur_i & \sim LogNormal(\mu_i, \sigma)\\ \mu_i & = \beta_0 + \beta_1 \cdot SR_{ctr[i]}\\ \end{align} \]

  • \(\beta_0\) is the intercept. This is the mean RT when centred speech rate is 0 (i.e. when speech rate is at its mean = NA).

  • \(\beta_1\) is the slope. This is the change in RT for each unit increase of centred speech rate (i.e for every unit increase of speech rate).

Regression model of vowel durations: code

dur_sr <- brm(
  v1_duration ~ 1 + speech_rate_c,
  family = lognormal,
  data = durations,
  cores = 4,
  seed = 1032,
  file = "data/cache/dur_sr"
)

Regression model: summary

summary(dur_sr)
 Family: lognormal 
  Links: mu = identity; sigma = identity 
Formula: v1_duration ~ 1 + speech_rate_c 
   Data: durations (Number of observations: 886) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Regression Coefficients:
              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept         4.72      0.01     4.71     4.74 1.00     4388     2452
speech_rate_c    -0.23      0.01    -0.25    -0.22 1.00     4482     2982

Further Distributional Parameters:
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma     0.22      0.01     0.21     0.23 1.00     3913     2983

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Interpreting the summary

\[ \begin{align} dur_i & \sim LogNormal(\mu_i, \sigma)\\ \mu_i & = \beta_0 + \beta_1 \cdot SR_{ctr[i]}\\ \end{align} \]

fixef(dur_sr)
                Estimate   Est.Error       Q2.5      Q97.5
Intercept      4.7230357 0.007580906  4.7081901  4.7379128
speech_rate_c -0.2344362 0.009378120 -0.2525304 -0.2157794

  • Intercept is \(\beta_0\): mean duration when speech rate is at mean.

  • speech_rate_c is \(\beta_1\): change in duration for each unit increase of speech rate.

Interpreting the summary: Intercept

fixef(dur_sr)
                Estimate   Est.Error       Q2.5      Q97.5
Intercept      4.7230357 0.007580906  4.7081901  4.7379128
speech_rate_c -0.2344362 0.009378120 -0.2525304 -0.2157794

  • The mean logged vowel duration is on average 4.72 (SD = 0.008).

  • There is a 95% probability that the mean logged vowel duration is between 4.71 and 4.74.

Interpreting the summary: speech_rate_c

fixef(dur_sr)
                Estimate   Est.Error       Q2.5      Q97.5
Intercept      4.7230357 0.007580906  4.7081901  4.7379128
speech_rate_c -0.2344362 0.009378120 -0.2525304 -0.2157794

  • The average change in logged vowel duration for each unit increase of speech rate is -0.23 (SD = 0.01).

  • In other words, for each increase of one syllable per second, the logged vowel duration decreases on average by -0.23.

  • We can be 95% confident that the decrease in logged duration is between -0.22 and -0.25.

Plotting the model predictions

conditional_effects(dur_sr)

Figure 3

Posterior predictive checks

pp_check(dur_sr, ndraws = 20)

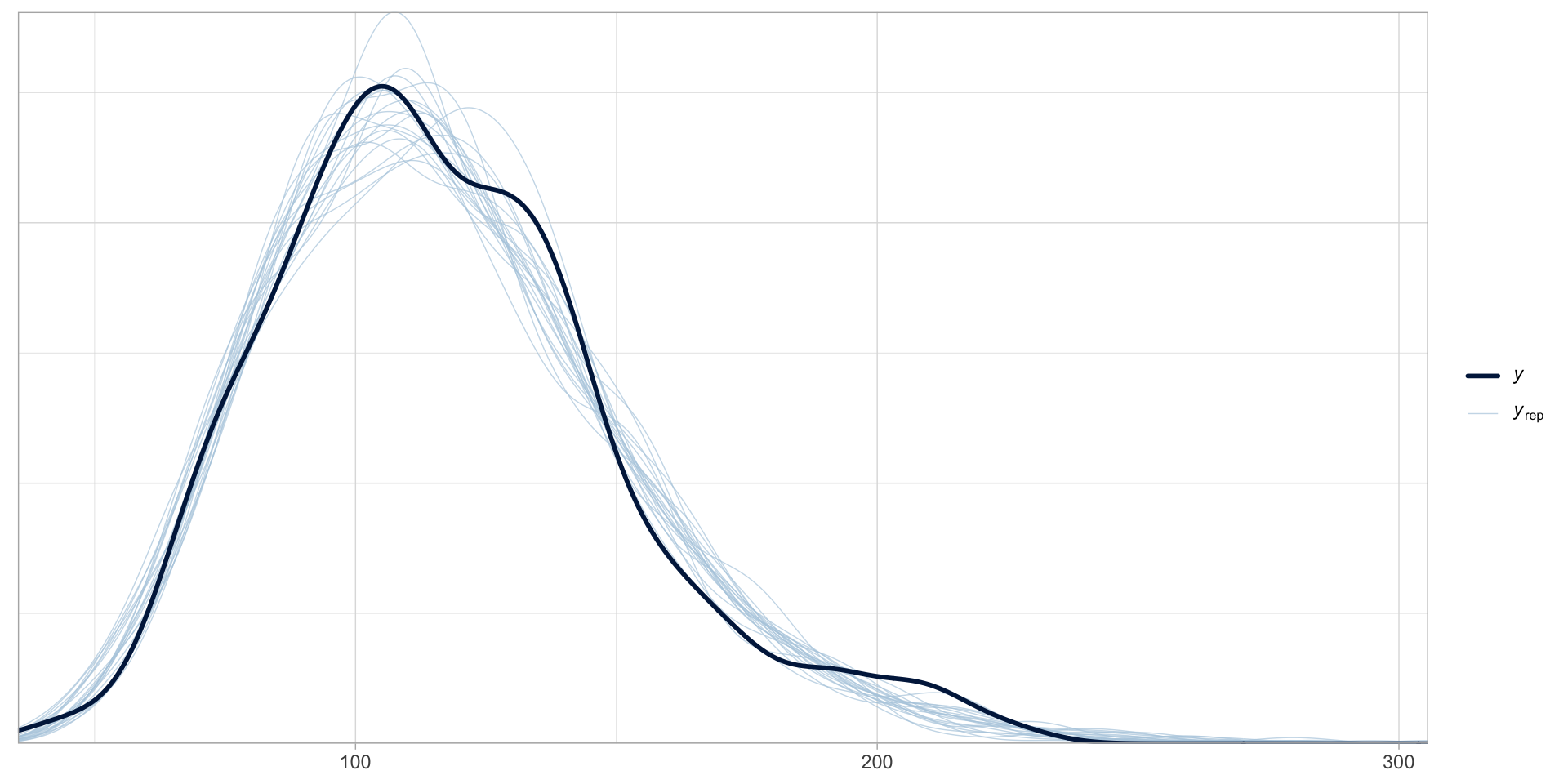
Figure 4: Posterior predictive check plot of dur_sr.

Summary

  • Regression models are models that use the formula of a line.

  • A simple regression model with one numeric predictor estimates the line’s intercept (\(beta_0\)) and slope (\(beta_1\)) and the overall standard deviation (\(sigma\)).

\[ \begin{align} y_i & \sim LogNormal(\mu_i, \sigma)\\ \mu_i & = \beta_0 + \beta_1 \cdot x \end{align} \]